주사위 하나를 던졌을 때 나오는 눈의 기대값이 3.5라는 것은 통계학개론, 기초확률론 강의에서 수도 없이 들었다. 근데 정말로, 진짜로 그것이 맞는지 내 두 눈으로 확인하지 않고서야 그냥 넘어가지 못하는 바보같은 성격 때문에 주사위 1000번(정확히는 1000개의 눈)을 던져 평균을 구해보았다. 그리고 믿을 수 없게도 결과는...
이제 읽게 되실 이 글은 통계학이 어려운 통계학과 학부 졸업생이 작성한 글로 오류가 상당 부분 존재할 예정입니다. 평균과 기대값은 엄밀히 따지자면 분명 차이가 있으나 본 글에서는 직관적인 의미전달을 위해 혼용하여 사용했습니다. 댓글 또는 메일 또는 유선전화 또는 인스타그램DM을 통해 적극적인 태클과 피드백을 부탁드립니다. 겸허히 받아들여 성장의 자양분으로 삼겠습니다.
잘하진 못했지만 학부에서 통계학을 공부하고 대학원에 입학했다. 지도교수님께서 통계과목은 빨리 끝내 놓으라는 말씀해주셔서 첫 학기부터 다시 통계학 과목을 수강하게 되었다. 광고를 전공 했다던 동기는 자신은 '통계 문외한'이라며 통계강의가 끝날 때면 나에게 다음과 같은 질문들을 했다.
"기대값이 뭔지 이해가 안가요"
"기대값도 정규분포일 것이라 가정하고 산출한 값인건가요?"
"주사위 기대값을 구하는 공식(1x1/6+2x1/6...6x1/6)에서 1~6은 정확히 어떤 의미인가요?"
어렵지도 않은 질문이었다. 통계학 난제에 대한 질문이 아니었기 때문이다. 그러나 나는 동기가 했던 위 질문 중 무엇하나 명쾌하게 대답해 줄 수 없었다. 질문의 수준이 아닌 쉽사리 질문에 대답할 수 없는 내 얄팍한 지식 수준 때문에 나는 말문이 턱 막혔다.
여지껏 살아오면서 주사위의 기대값을 진짜로 궁금해한 적은 단 한번도 없었고 단지 통계학 교재에서 수도 없이 나왔기 때문에 그냥 "주사위의 기대값은 3.5"라고 기계적으로 받아들이고 있었음을 깨달았다.
과거 통계학자들은 왜 주사위와 동전으로부터 확률론을 펼쳐 나갈 수 있었는지, 그것이 무슨 의미가 있어서 2020년인 지금에도 통계학 교재에는 주사위의 기대값에 대한 이야기가 나오는 것인지, 나는 고민하지 않았다. 100~200년 전 통계학자들의 사고 흐름을 조금도 따라간적이 없었기 때문에 근본적인 것에 대한 물음에 대답할 수 없었다는 것을 깨달았다.
그래서 진짜로, 정말로, 진실되게 주사위의 기대값은 3.5인지에 대해 경험적 방법을 통해 확인하고자 마음을 먹었다.
쿠팡에서 주사위 세트를 주문하여 다음과 같은 확률실험(random experiment)을 진행했다.
실험 동기
•
주사위의 기대값은 정말로 3.5인가? 아니, 정말 3.5에 가깝기라도 한 것일까?
실험 목적
•
위 질문에 답을 구한다. 주사위 던지기를 1000번 시행하여 큰수의 법칙(law of large number)에 따라 평균이 3.5에 가까워지는지 확인한다.
실험 방법
•
주사위 10개를 100번 던진다. (주사위 던지기를 1개를 1번씩 하지 않은 것은 단지 편의를 위함이었다.)
•
1시행(주사위 10개x10번)마다 나온 주사위의 눈을 엑셀에 기록한다.
실험 도구
ⓐ 주사위
•
정육면체 주사위 10EA
•
주사위 크기: 1.4cm X 1.4cm X 1.4cm
•
주사위 무게: 19g
•
원산지: 중국
ⓑ 기초확률론 제 3판, 신양우 지음 (경문사)
•
주사위를 던질 때 받침대로 활용하였다.(교재 비하 의도는 전혀 없으며 단지 본 교재로 공부하던 중 호기심에 바로 책을 뒤집어 본의 아니게 책을 받침대로 사용하게 되었습니다. 죄송합니다.)
실험 일자 및 장소
•
2020년 10월 1일 2:30 ~ 3:30
•
한양대학교 서울캠퍼스 제 2학생생활관 1층 식당
실험 특이사항
•
주사위를 굴리는 데 너무 시끄러웠던 나머지 옆 자리의 유학생이 굉장히 눈치를 많이 주었다.
대망의 실험 결과
정확한 평균은 3.45
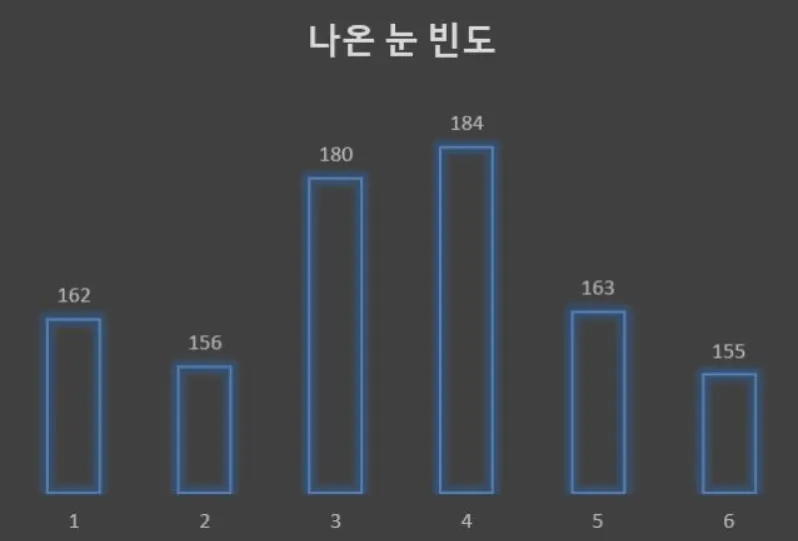
각 눈이 나온 빈도는 다음과 같다.
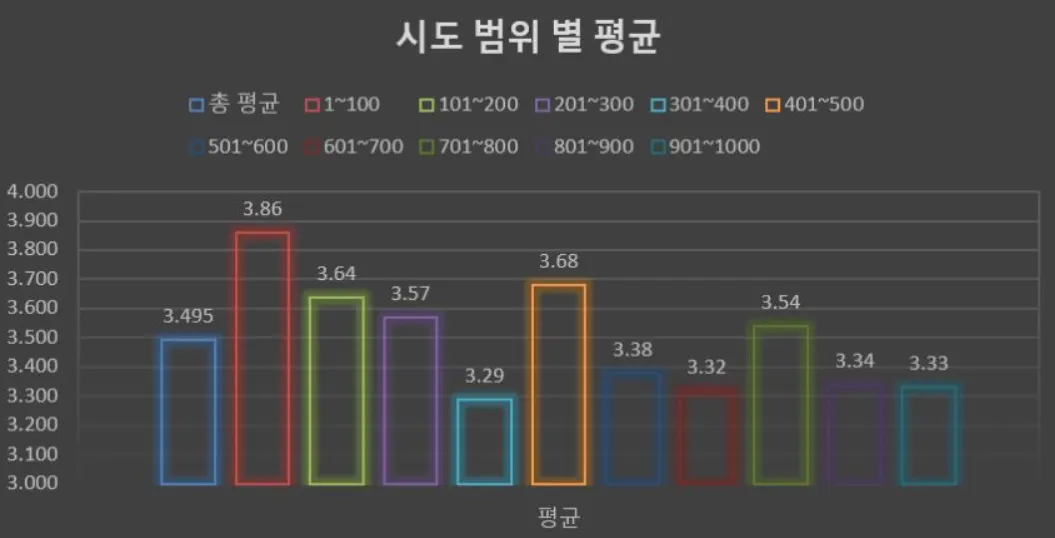
각 10번의 시행 구간 별(주사위 10개x10번=총 100개의 눈) 평균은 다음과 같다.
개신기하다!