Search

표준화 가중치

표본의 대표성을 높이는 통계적인 기법: 표준화 가중치

1. 표준화 가중치를 적용했다!?

1.1. 사회 분야의 조사 결과에 빈번히 등장하는 ‘표준화 가중치’

•
道 여성 6명 중 1명, 성희롱 피해 경험 3명 중 1명 (2023년 3월 8일, 경기매일, 황영진 기자)
위 기사는 2022년 9월~10월까지 경기도내 19세~75세 성인 2,000명을 대상으로 실시한 ‘경기도 여성폭력 실태조사’에 관한 기사인데, 기사의 마지막 부분에는 다음과 같이 기재되어 있습니다.[1], [2]
*본 조사는 표준화 가중치를 적용해 성비가 1:1에 근접하게 조정했음 (전체 사례수 2,000명 중 남성 1,019명, 여성 981명 대상)
공공기관의 수많은 조사결과에서 ‘표준화 가중치’를 적용했다는 문구가 빈번히 등장하지만 그 개념을 함께 설명해주는 경우는 거의 없기 때문에 어떻게 해석해야 할지 가늠할 수 없는 경우가 많습니다.
조사 결과를 활용하는 실무자 입장에서 표준화 가중치에 대한 개념을 함께 이해할 수 있는 글을 작성하고자 합니다.

2. 표본 가중치의 역할과 필요성

2.1. 표본 가중치의 정의

표본 가중치란 한 표본이 몇 개를 대표하는가
일상에서 어떤 것에 대해 “높은 가중치를 부여했다”라는 것은 그만큼 중요하다고 보고 있다로 해석합니다. 국립국어원의 표준국어대사전에서는 그런 가중치를 “일반적으로 평균치를 산출할 때 개별치에 부여되는 중요도”라고 정의하였다습니다. [3]
그렇다면 ‘표본 가중치’는 무엇일까요?
세계보건기구(WHO)에서 실시하는 Global Adult Tobacco Survey(GATS)의 표본 가중치 메뉴얼(Sample Weights Manual)에서는 표본 가중치에 대해 “응답자에 대한 데이터를 얻을 수 있는 확률의 역수”라고 정의하였습니다. [4]
확률과 역확률에 대한 내용은 후술하고 위 두 개의 정의를 정리해보면 표본 가중치는 추론 통계에서 특정 표본의 상대적인 ‘중요성’을 나타내는 값이라고 볼 수 있습니다.

2.2. 표본 가중치의 필요성

일반적으로 우리는 모집단을 잘 설명해줄 표본을 추출하기 위해 표본의 특성 비율이 모집단과 일치하도록 표본을 추출합니다. 그러나 무작위로 추출되는 표본이 모집단을 ‘완벽하게’ 대표하지는 못합니다. 이러한 표본과 모집단의 특성 간 차이를 표본 오차(sampling error)라고 하며 이 표본오차는 표본의 크기, 추출 방법, 모집단의 특성 등 여러 요소에 의해 영향을 받습니다.
이러한 표본 오차가 발생하면 표본이 모집단의 특성과 일치하지 않게 되어 추정하는 정확성이 떨어지는 문제가 발생합니다. 따라서 원래는 더 추출되었어야 했으나 덜 추출된 표본에는 가중치를 더 부여하고, 원래는 덜 추출 되었어야 했으나 더 추출된 표본에 대해서는 가중치를 적게 부여하여 표본 오차를 통제합니다.
개괄적으로 정리해보면 표본 가중치의 필요성은 아래와 같습니다.
•
모집단의 특성을 반영
일반적으로 표본을 추출할 때, 모집단의 특성을 대표하는 표본을 추출하기 위해 무작위 추출 방법(Random Sampling)을 사용합니다. 그러나 조사 기간, 비용 등 경제적인 이유나 현저하게 낮은 응답률 등 현실적인 이유로 추출된 표본들 역시도 모집단의 특성을 완벽하게 반영하지 못할 수 있습니다. 표본 가중치는 모집단의 특성에 맞춰 표본 특성을 조정함으로써 표본의 대표성을 높여줍니다.
•
무응답 보완
조사 과정에서 일부 응답자 또는 집단이 설문에 응하지 않는 경우가 발생합니다. 이러한 무응답은 표본이 모집단을 완벽하게 대표하지 못하게 되는 이유 중 하나입니다. 따라서 표본 가중치를 사용하여 응답률이 낮은 집단에는 높은 가중치를 부여하여 무응답에 대해 보정합니다.
•
계층적인 구조
조사 대상인 모집단이 여러 개의 계층으로 나뉘어 있는 경우, 각 계층에서 표본의 크기와 선택 확률이 다를 수 있습니다. 이런 경우 표본 가중치를 통해 각 계층의 중요성을 반영하여 계층별 추정치를 조정할 수 있습니다.

3. 표본 가중치의 계산 방법

3.1. 추출 방법에 따른 표본 가중치 계산

표본을 추출하는 방법에 따라 표본 가중치를 계산하는 방식 역시 다릅니다.
단순확률 추출법에서는 가중치가 동일하게 설정됩니다. 계통추출법에서 표본 가중치는 전체 개체 수에 대한 표본 크기의 역수로 계산됩니다. 층화확률추출법에서는 층 내 개체 수에 대한 표본 크기의 역수와 층의 비율의 역수의 곱으로 가중치를 계산합니다. 집락추출법에서는 전체 집락 수에 대한 표본 집락 수의 역수를 가중치로 사용합니다. 이러한 가중치는 표본 추출 시 모집단의 특정 부분을 잘 반영하며, 통계적 추론과 모집단 추정에 정확성을 높일 수 있습니다.
추출 방법
설명
표본 가중치 계산 방법
① 단순확률 추출법 (Simple Random Sampling)
모든 개체가 동일한 확률로 선택되는 경우
1/추출된 표본의 비율 = n/N
② 계통추출법 (Systematic Sampling)
일정한 간격으로 개체를 선택하는 경우
전체 개체 수 / 표본 크기 = N/n
③ 층화확률추출법 (Stratified Random Sampling)
모집단을 여러 층으로 구분하고 각 층에서 표본을 추출하는 경우
(층 내 개체 수 / 표본 크기) * (층의 비율의 역수)
④ 집락추출법 (Cluster Sampling)
모집단을 집락(클러스터)으로 구분하고 일부 집락을 선택하여 집락 내 개체를 모두 포함하는 경우
전체 집락 수 / 표본 집락 수

3.2. 표본 가중치의 종류

표본 가중치는 다양한 조사와 그 목적에 맞춘 여러 가지의 가중치가 있습니다. 주요 표본 가중치의 종류는 다음과 같습니다.
① 확률 가중치 (Probability Weight)
•
일반적으로 가장 많이 사용되는 표본 가중치
•
각 개체의 선택 확률을 반영하여 가중치를 부여
•
가중치는 개체의 역수로 계산되며, 선택 확률이 높을수록 가중치가 작아짐
② 설문응답 가중치 (Survey Response Weight)
•
설문조사에서 응답률을 조정하기 위해 사용되는 가중치
•
응답률이 낮은 그룹에 가중치를 더 부여하여 전체 응답자 대표성을 향상시킴
•
일반적으로 가중치는 응답률과 비례하여 계산
③ 사후층화 가중치 (Poststratification Weight)
•
모집단의 특정 층별 구성 비율과 표본의 층별 구성 비율을 조정하기 위한 가중치
•
표본 추출 후 모집단의 특성을 고려하여 가중치를 조정하여 추정값을 보정
④ 이중 층화 가중치 (Dual Frame Weight)
•
두 개 이상의 층화 구조에서 표본을 추출하는 경우 사용되는 가중치입니다.
•
예를 들어, 전화와 인터넷을 통한 조사에서 각각의 층에서 표본을 추출할 때 사용됩니다.
•
각 층의 가중치를 조정하여 전체 모집단을 대표하는 추정치를 계산합니다.
최종 가중치 w는 조사 목적에 따른 필요한 표본 가중치의 종류에 따라 필요한 가중치를 곱해 결정합니다.
w=w1×w2×...×wnw = w_1 \times w_2 \times ... \times w_n

3.3. 예제

실제 저희 부서에서 실시했던 조사를 일부 수정하여 표본 가중치를 구해보겠습니다.
특정 서비스의 사용량에 대한 조사로 전국 만 20세 이상 64세 이하 성인을 대상으로 실시하였습니다.
이번 예제에서는 편의상 서울, 경기로 국한지어 표본 가중치를 구해보겠습니다.

전국 OO 서비스 사용량 조사

지역
모집단
표본크기
추출률
설계가중치
응답률
응답가중치
서울
6,372,567명
200명
1/31863
31863
5%
20
경기
9,089,795명
300명
1/30299
30299
8%
12.5
① w1: 설계가중치 (확률가중치, Probability Weight)
각 객체의 선택확률을 반영하는 확률가중치를 먼저 구해보겠습니다. 행정안전부의 통계에 따르면 2023년 3월 기준 서울과 경기에 거주 중인 만 20세 이상 만 64세 이하 성인 남녀의 인구수는 아래와 같습니다.
•
서울 또는 경기에 거주 중인 만 20세 이상 만 64세 이하 성인 남녀
◦
2023년 3월 기준
▪
서울: 6,372,567명
▪
경기: 9,089,795명
조사 결과 서울과 경기에 거주 중인 응답자는 각각 200명과 300명이었습니다. 최종 응답자와 실제 모집단의 크기를 활용해 추출률을 계산하겠습니다.
•
추출률
◦
서울
nN=2006372567=131863{n \over N} = {200\over6372567} = {1\over 31863}
◦
경기
nN=3009089795=130299{n \over N} = {300\over 9089795} = {1\over 30299}
•
설계가중치 (확률가중치, Probability Weight) : W1
◦
서울: 31,863→ 서울 표본 1명 당 31,863명 대표
◦
경기: 30,299 → 경기 표본 1명 당 30,299명 대표
② w2: 응답가중치 (설문응답 가중치 , Survey Response Weight)
두 번째 가중치로 응답가중치를 구해보겠습니다. 설문조사에서 응답률을 조정하기 위해 사용되는 가중치로 응답률이 낮은 그룹에 가중치를 더 부여하여 전체 응답자 대표성을 향상시킵니다.
조사 결과 서울과 경기의 응답률은 아래와 같습니다.
•
응답률
◦
서울: 응답률 5%
◦
경기: 응답률 8%
응답가중치는 응답률의 역수로 5%와 8%의 역수는 각각 20과 12.5입니다.
•
응답가중치 (설문응답 가중치 , Survey Response Weight): W2
◦
1/응답률
◦
서울: 응답가중치 20 → 서울 응답자 1명당 20명 대표
◦
경기: 응답가중치 12.5 → 경기 응답자 1명당 12.5명 대표
③ w3: 사후층화 가중치 (Poststratification Weight)
마지막 가중치는 사후층가중치입니다. 사후층화가중치는 모집단의 특정 층별 구성 비율과 표본의 층별 구성 비율을 조정하기 위한 가중치로 표본 추출 후 모집단의 특성을 고려하여 가중치를 조정함으로써 추정값을 보정해줍니다.
인구 통계에 따르면 서울과 경기의 성비는 아래와 같습니다.
•
서울: 남자 49%, 여자 51%
•
경기: 남자 51%, 여자 49%
사후층화 가중치는 각 층의 비율을 표본의 비율로 나눈 값으로 계산합니다. 인구 통계에 따르면 서울과 경기 모두의 성비 남성 50%, 여성 50%입니다. 표본에서의 성비는 여성 49%, 남성 51%입니다.
성비에 따른 사후층화 가중치를 구하면 아래와 같습니다.
•
남성: (모집단의 남성 비율 / 표본의 남성 비율) = (51% / 50%) = 1.02
•
여성: (모집단의 여성 비율 / 표본의 여성 비율) = (49% / 50%) = 0.98
최종 가중치는 w는 다음과 같습니다.
w=w1×w2×w3=설계가중치×응답가중치×사후층화가중치w = w_1 \times w_2 \times w_3 = 설계가중치 \times 응답가중치 \times 사후층화 가중치
•
응답한 서울 남자
31863×20×1.02=65000531863 \times 20 \times 1.02 = 650005
•
응답한 서울 여자
31863×20×0.98=624515 31863 \times 20 \times 0.98 = 624515
•
응답한 경기 남자
30299×12.5×1.02=386312 30299 \times 12.5 \times 1.02 = 386312
•
응답한 경기 여자
30299×12.5×0.98=37116330299 \times 12.5 \times 0.98 = 371163
가중치를 구했으니 OO 서비스의 사용량에 실제 가중치를 적용해보겠습니다.
지역과 성별에 따른 OO 서비스의 하루 평균 사용량은 다음과 같습니다.
•
응답한 서울 남자: 20분
•
응답한 서울 여자: 5분
•
응답한 경기 남자: 25분
•
응답한 경기 여자: 10분

4. 표준화 가중치

이 글의 작성 이유이자 첫 번째 질문은 “표준화 가중치는 무엇이고 어떻게 해석해야 하는가?”였습니다.
표준화 가중치는 위와 같이 구한 표본 가중치를 표준화(Standardization)한 것으로 앞서 설명 드린 사후층화 가중치(Poststratification Weight)의 한 종류입니다.

4.1. 표준화 가중치의 정의

최종 가중치를 응답된 표본크기에 맞춰 표준화하여 분석과 해석의 용이성 제고 [5]
한국갤럽에서는 매주 금요일 오전 10시 ‘데일리 오피니언’이라는 통계 조사 결과를 발표합니다. 전화조사를 통해 대통령 직무수행평가와 정당 지지도, 기본 국정 지표와 주요 정치 현안, 경제, 사회, 생활, 문화 등 다방면에 관한 국민들의 생각을 물어 집계 및 분석합니다. [5]
한국갤럽의 데일리 오피니언은 거주지, 성별, 연령대를 변수로 층화하여 인구 수에 비례하여 표본을 추출하는 비례층화추출(proportional stratified sampling) 방식을 통해 표본을 추출합니다.
설계된 표본에 맞춰 무작위로 전화번호를 생성(Random Digit Dialing, RDD)하여 전화조사를 수행한 뒤 필요에 따라 사후층화 가중치를 적용합니다. 이렇게 산출된 최종가중치를 응답된 표본 크기에 맞춰 표준화합니다. [5] 표준화 가중치는 가중치의 합계가 표본 크기와 같아지도록 최중 가중치를 변환한 것입니다. [6]

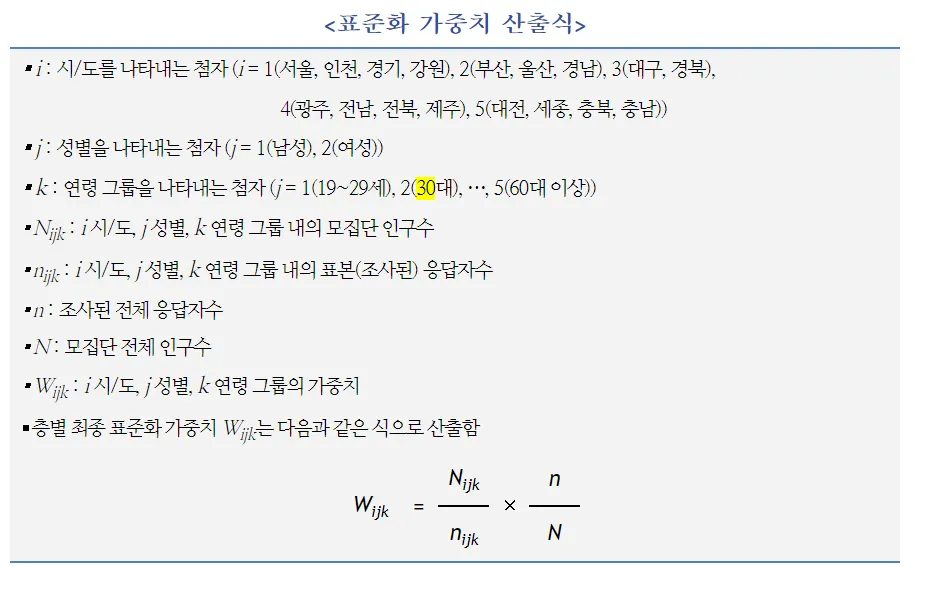
4.2. 표준화 가중치 산출식

5. 표준화 가중치의 활용

6. 참고 문헌

[1] 황영진. “道 여성 6명 중 1명, 성희롱 피해 경험 3명 중 1명”, 경기매일, 08.03.2023, http://www.kgmaeil.net/news/articleView.html?idxno=316522.
[2] “경기도여성가족재단. 2022. 『경기도 여성폭력 실태조사 』 81 쪽"
[4] Global Adult Tobacco Survey Collaborative Group. 2010b. Global Adult Tobacco Surveys (GATS): Sample Weights Manual <www.cdc.gov/tobacco/global/gats>.
[5] Gallup Korea. (2020, October 15). 2020년 대한민국의 성비 추정. [웹페이지]. 2023년 6월 4일에 접속 https://www.gallup.co.kr/gallupdb/columnContents.asp?seqNo=123
[6] 권희경. (2020). 2020 KEDI 학생역량 조사 연구 (RR2020-29). [KEDI] 연구보고서.